6.1.2.График и својства (дефинициона област, множество вредности, монотоност, пресечни точки со координатните оски)

Постојат повеќе дефиниции за линеарна функција во светот.

• Линеарна функција се дефинира како полиномна функција од прв степен од една независно променлива х , од што следува дека:
  • Во експлицитен облик имаме:   ${\displaystyle f(x)=ax+b}$  или  ${\displaystyle y(x)=ax+b}$  или  ${\displaystyle y=ax+b,\,a\neq 0}$.
  • Бидејќи тука а≠0, опаѓаат константни функции (хоризонтални прави) и остануваат само коси прави во рамнината.
  • Оваа дефиниција има природно место помеѓу константна функција и квадратна функција.

• Линеарна функција се дефинира како функција чиј графикон е права во рамнина, од што следува дека:
• Во експлицитен облик имаме:   ${\displaystyle f(x)=ax+b}$  или  ${\displaystyle y(x)=ax+b}$  или  ${\displaystyle y=ax+b}$.
• Во оваа дефиниција се вклучени и хоризонтални прави y=b, односно константни полиноми. (Вертикални прави x=b не се функции.)
• Забелешка: оваа дефиниција е без условот a≠0.

Дефинициона област 

или доменот на линеарната функција е целото множество реални броеви. Множеството на допуштени вредности на секоја линеарна функција е R, т.е. сите реални броеви. Значи, било кој реален број може да „влезе“ во линеарна функција, односно да биде замената за х во функцијата. 

Множество вредности

или кодоменот на линеарната функција е целото множество реални броеви. Сликата, т.е. множеството на сите излезни вредности исто така е R, т.е. сите реални броеви.

Монотоност

Да ги разгледаме сега графиците на линеарните функции у=2х+1 и у=-2х+1 

• при зголемување на вредностите на независната променлива х се зголемува и вредноста на зависната променлива у
• при зголемување на вредностите на независната променлива х се намалува вредноста на зависната променлива у

Дефиниција: Линеарната функција е растечка ако зголемувањето на вредностите на независната променлива условува зголемување на вредностите на зависната променлива

Дефиниција: Линеарната функција е опаѓачка ако зголемувањето на вредностите на независната променлива условува намалување на вредностите на зависната променлива

Заклучок: 

• Ако бројката пред х е позитивна т.е. (а>0), тогаш функцијата е растечка, а нејзиниот график зафаќа остар агол со позитивниот дел на х-оската
• Ако бројката пред х е негативна т.е. (а<0), тогаш функцијата е опаѓачка, а нејзиниот график зафаќа тап агол со позитивниот дел на х-оската 

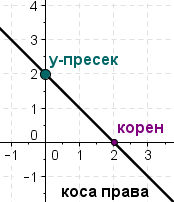
Пресечни точки со координатните оски

Дефиниција: Вредноста на независната променлива за која вредност функцијата (зависната променлива) е еднаква на нула се нарекува корен на функцијата (или нула на функција).

Дефиниција: Вредноста на зависната променлива за која вредноста на независната променлива е еднаква на нула се нарекува у-пресек на функцијата (или пресек со у-оската).

Задача:

Да ги најдеме пресечните точки на линеарната функција y=3x-6 со координатните оски

Пресекот со у-оската е во точката (0,-6)

Како е најдена точката?

Во функцијата за х даваме вредност 0 т.е. х=0 и добиваме у=3∙0-6=0-6=-6.

Пресекот со х-оската е во точката (2,0)

Како е најдена точката?

Во функцијата за у даваме вредност 0 т.е. у=0 и добиваме 0=3∙х-6 ја решаваме оваа равенка 

-3х=-6 ⟺ х=-6:(-3) ⟺ х=2

Задачи за домашна работа:

1. Напиши, пет линеарни функции кои рамномерно растат.
2. Напиши, пет линеарни функции кои рамномерно опаѓаат
3. На функцитте кои рамномерно растат пронајди ги корените.
4. На функциите кои рамномерно опаѓаат пронајди ги пресеците со у-оска.