Процес на решавање линеарна равенка
- Ако равенката има дропка т.е. содржи броеви за именители, искористете го најмалиот заеднички именител за да се ослободите од овие именители. Ние тоа ќе го сториме со множење на двете страни на равенката со НЗС(именителите).
- Исто така, ако дропката има променливи во именителите ги идентификуваме вредностите на променливата кои ќе дадат делење со нула на дропката, бидејќи е потребно да ги изоставиме овие вредности во нашето решение
- Поедноставете ги двете страни на равенката. Ова значи да се ослободиме од заградите и да ги комбинираме како изрази.
- Користејќи ги својствата за еквивалентни равенки направете сите изрази со променлива да бидат на една (обично левата) страна на равенката (комбинирајќи ги во еден израз се разбира) и сите константи од другата (обично десната) страна на равенката.
- Значи ќе ја добиеме равенката во стандардна форма (ax=b).
- Важно е да забележиме дека во вака добиената равенка ги делиме двете страни на равенката со коефициентот пред променливата, ако тоа е цел број или ги множиме двете страни на равенката со реципрочната вредност на коефициентот ако тоа е дропка.
- ВЕРИФИКАЦИЈА НА ВАШИОТ ОДГОВОР! Ова е последниот чекор и најчесто прескокнат чекор, но сепак ова е веројатно и најважниот чекор во процесот. Со овој чекор можете да знаете дали го имате точниот одговор долго пред вашиот наставник некогаш да го погледне тоа. Го потврдуваме одговорот со внесување на резултатите од претходните чекори во првобитната равенка. Многу е важно резултатите да ги внесете во првобитната равенка бидејќи можеби сте направиле грешка во првиот чекор и тоа ве донело до неточен одговор.
- Исто така, ако имало дропки во проблемот и имало вредности на променливата што даваат делење со нула (потсетете се на вториот чекор ...), важно е да бидете сигурни дека една од овие вредности не завршила во пресметаното решение. Бидејќи можно е, некои од овие вредности да бидат решение на равенката.
Пример 1
Реши ја равенката:
3(x+5)=2(−6−x)−2x
Решение:
Равенката нема дропки, затоа првите два чекора од процесот ги прескокнуваме, одиме на третиот чекор и добиваме:
3х+15=−12−2x−2x
Сега сите изрази кои имаат х да се најдат на левата страна на равеката (ако не се наоѓаат таму, ги носиме таму но со спротивен знак), а сите константи сакаме да се најдат на десната страна на равенката (ако не се наоѓаат таму, ги носиме таму но со спротивен знак)
3х+2x+2x=−12−15
7х=−27 /:(7)
х=−(27/7)
Пример 2
Реши ја равенката:
Решение:
Решение:
Најпрвин ги разложуваме именителите на дропките на множители
Равенката има дропки и тоа дропки со променливи во именителирте, затоа почнуваме од првиот чекора од процесот. Бараме НЗС(2(y-3),(y-3)(y-3)) и добиваме
Решение:
Равенката има дропки, затоа почнуваме од првиот чекор од процесот. Бараме НЗС(3,7) и добиваме НЗС(3,7)=21.
Во именителите нема променливи затоа го прескокнуваме вториот чекор. Одиме на третиот чекор од процесот, значи да се ослободиме од заградите.
Проверка: Ако во првобитната равенка замениме m=−7 добиваме:
Во именителите нема променливи затоа го прескокнуваме вториот чекор. Одиме на третиот чекор од процесот, значи да се ослободиме од заградите.
Проверка: Ако во првобитната равенка замениме m=−7 добиваме:
Пример 3
Реши ја равенката:
Најпрвин ги разложуваме именителите на дропките на множители
НЗС(2(y-3),(y-3)(y-3))=(2(y-3)(y-3)) Да забележиме дека равенката не смее да има решение y=3 бидејќи за таа вредност имаме делење со нула.
Проверка: Ако во првобитната равенка замениме y=5 добиваме:
Проверка: Ако во првобитната равенка замениме y=5 добиваме:
Пример 4
Решение:
Равенката има дропки и тоа дропки со променливи во именителирте, затоа почнуваме од првиот чекора од процесот. Бараме НЗС(z+3,z-10) и добиваме НЗС(z+3,z-10)=(z+3)(z-10) . Веднаш да забележиме дека равенката не смее да има решенија z=-3 и z=10 бидејќи за овие вредности имаме делење со нула.
Потребно е да согледаме дека добивме степен 2 на променливата z, но и гледаме дека ова може да се скрати, бидејќи имаат исти знаци а се наоѓаат од спротивни страни на равенката.
Проверка: Ако во првобитната равенка замениме z=17/3 добиваме:











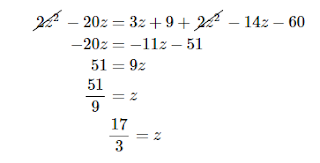



No comments:
Post a Comment