8.2.4.Три теореми (Евклидова, Питагорова и Талесова) за правоаголен триаголник

https://mk.wikipedia.org/wiki/%D0%9F%D0%B8%D1%82%D0%B0%D0%B3%D0%BE%D1%80%D0%BE%D0%B2%D0%B0_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0

Евклидова теорема

Во книгата I (еден) од Евклидови елементи во тврдењето под број 47 стои дека:

Во правоаголните триаголници , плоштината на спротивната страната  од правиот агол е еднаква на збирот на квадратите на страните што содржат правиот агол.

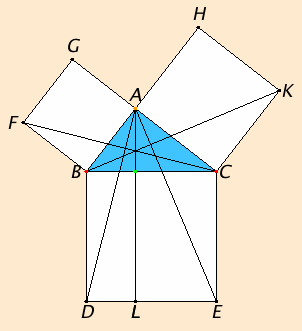
Доказ:

Доказот можете да го погледнете на веб страната:
https://mathcs.clarku.edu/~djoyce/java/elements/bookI/propI47.html

Питагорова теорема

c² = a² + b² – т.е. Плоштината на квадратот изграден од хипотенузата на правоаголен триаголник е еднаква на збирот на плоштините на квадратите изградени  од неговите катети.

Доказ:
Има повеќе докази, кои можете да ги погледнете на веб страната:
https://mk.wikipedia.org/wiki/%D0%9F%D0%B8%D1%82%D0%B0%D0%B3%D0%BE%D1%80%D0%BE%D0%B2%D0%B0_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0

Талесова теорема

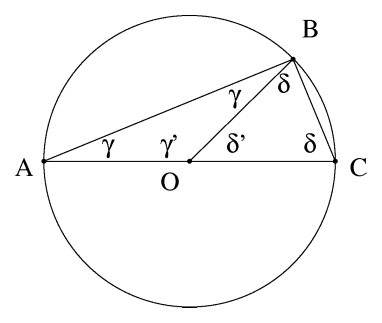
Во геометријата, Талесова теорема (го добила името по Талес од Милета) Ако А,В и С се точки во кругот каде што АС е дијаметар на кругот, тогаш аголот АВС е прав агол.

Доказ:

Ја користиме претпоставката дека: збирот на аглите во триаголникот е еднаков на збирот на два прави агли и два агли кај рамнокрак триаголник се еднакви

Нека O е центар на кругот. Нека OA = OB = OC, OAB и OBC се рамнокраки триаголници, и од еднаквоста на аглите на рамнокракиот триаголник, OBC = OCB и BAO = ABO. Нека γ = BAO i δ = OBC.

2γ + γ ′ = 180°

и

2δ + δ ′ = 180°

Исто така знаеме, дека

γ ′ + δ ′ = 180°

Ако ги собереме првите две равенки, а ја одземеме третата, добиваме: 

2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°

што после скратување , γ ′ и δ ′, докажува дека

γ + δ = 90°